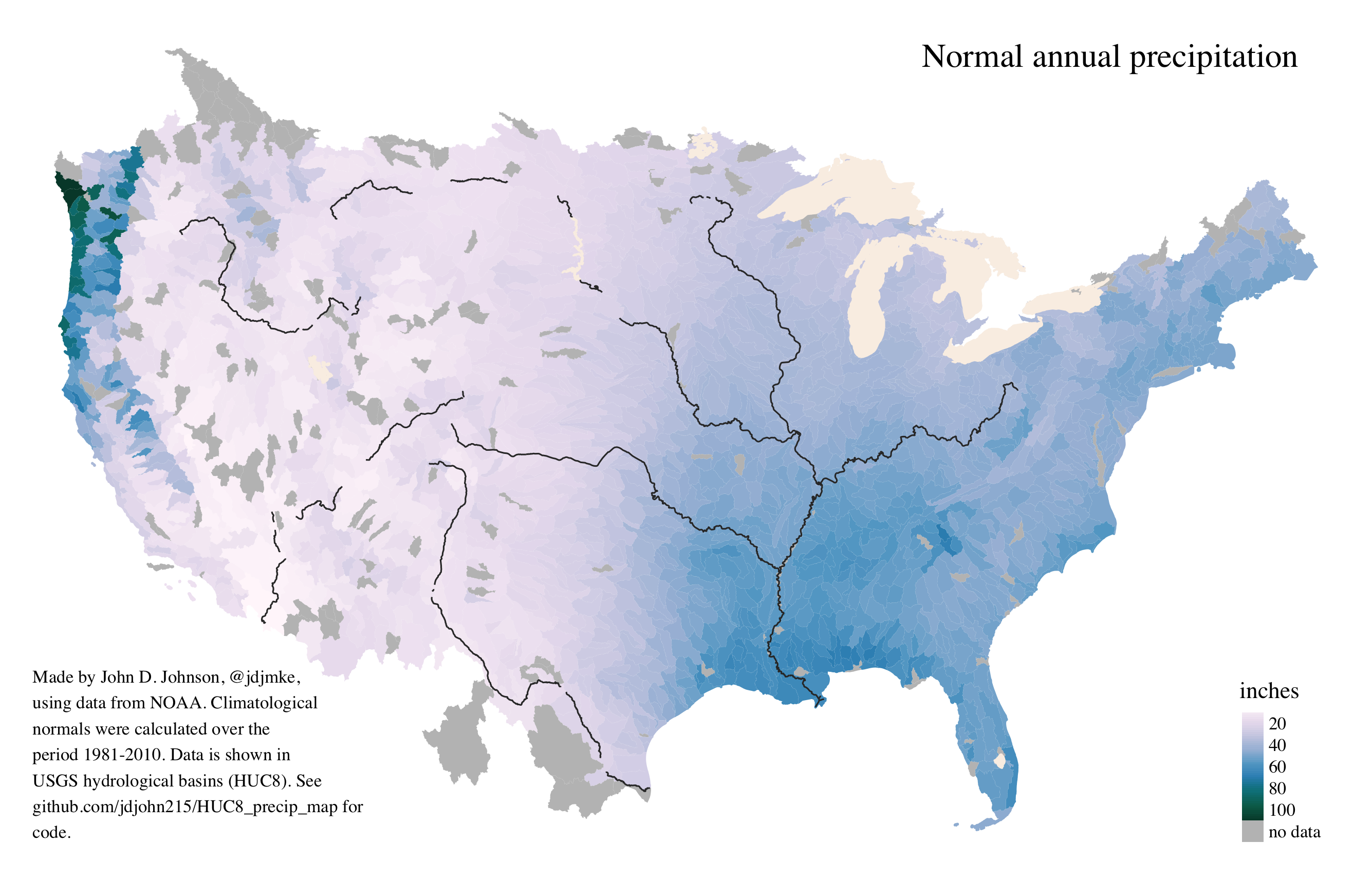
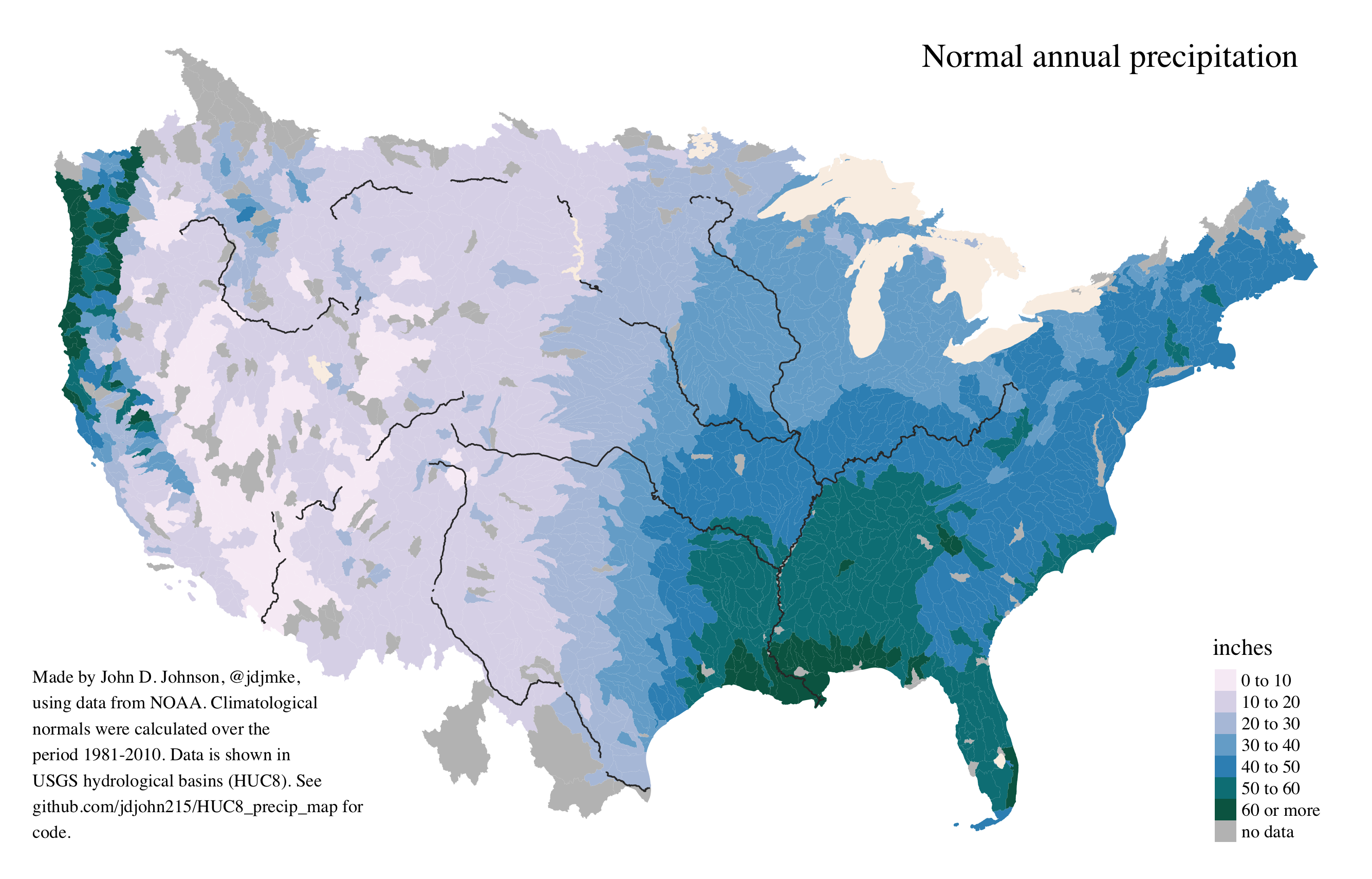
Maps of average rainfall in hydrological basins
A good map has to balance competing objectives. It should be coherent at first glance but still complex enough to reward careful examination. A good map invites the viewer in, often by giving them a personal frame of reference that they can then expand outwards to discover new information. Like all data visualizations, it exists to simply data, but it should do so in a way that informs, rather than misleads.
Often, maps just aren’t the right tool for the job. Maps are a terrible way to communicate election results, for instance. The point of an election map should never be to show you who won the election. If that is the goal, just use a table. Election maps are a good way to show who won an election and by how much in a given location, but in my experience, insisting that viewers interpret a map in the way you intend rarely works. The temptation to compare surface areas is just too great. Probably the best solution is just to offer a series of maps, each more accurate along a specific dimension of the truth. That’s the idea behind Ken Field’s gallery of 32 different kinds of 2016 election maps.
By the standards I’ve just described, I freely admit that most of my maps are bad. But here are two that I’m quite pleased with. All the data and code needed to create them are available in this github repo.
These maps contain no political boundaries except those which happen to follow natural features. Instead, they show average levels of precipitation in hydrological basins–the category one size up from watersheds. The first map shows a continuous scale. The dryest basin receives the lightest hue, and the wettest basin displays the darkest shade. The second map shows a binned scale. Although the binned map makes it easier to see patterns, it also creates two kinds of error. On the one hand it suggests an abrupt change in places where there is only a gradual shift. On the other, it also flattens outliers by incorrectly suggesting that the Mississippi River delta is as wet as the Olympic Peninsula.